
The dark energy and matter that drives economic performance
Innovation, like dark matter, can’t be measured well, but regional science is getting closer
Co-Director, Indiana Business Research Center, Indiana University Kelley School of Business
Anyone reading this article or anyone who decided not to read it, quits in the middle of reading it, or doesn’t even know the article exists, is a part of the 5%. Only 5% of the universe is observable and directly measurable. The rest of the universe is something of a head scratcher for most of us—dark energy and dark matter.
In a similar way, measuring innovation is a challenge. We’ll hear more and more about the importance of innovation in the coming years as a driver of economic growth, especially from political and thought leaders. But talk as they may, few can figure out how to measure it even remotely close to real time. Economists, business analysts and economic developers, to name a few, can observe it after it has happened, but getting a signal as it emerges and produces new products and creates new jobs is tricky.
We can observe innovation after it has happened, but getting a signal as it emerges and produces new products and creates new jobs is tricky.
A common, generally accepted measure for innovation is the count and rate of patent production. Another measure might be the rate of entrepreneurship, or new business formation, especially in the industry sectors that produce and apply new patent technologies. Others interested in the development, application and commercialization of knowledge might look at university or federal research laboratory collaborations with private industry as an indicator of innovation activities. All of these metrics have merit, if one can get good data for them. But even still, there is still a lot of innovation dark matter beyond our ability to measure and understand.
The IBRC has published an innovation index over the last decade (see StatsAmerica.org). The first index iteration was rather simple, e.g., counting the number of patents or the STEM occupations in a region. In the second iteration, the IBRC expanded the offerings of measures, including proxy measures for knowledge spillovers from universities or investments in new production facilities. While StatsAmerica will soon publish its next iteration of an innovation index—what we are going to call Innovation Intelligence—this isn’t an introduction to the new tool and data. That will be announced later in 2021.
This article describes and distills recent research that measures innovation and how we may apply it to Indiana. What we call innovation dark matter, professors Goetz and Han (2020) call “latent innovation.” (View their article.) We hope that our translation of the article does not do violence to their work or reputation. We hope that the description of the concepts make their work more accessible as we wrap our heads around innovation dark matter.
“Innovation theory,” if there is such a thing
In simple speak, innovation is making something better or new. Selling innovation on the open market—commercializing innovation—also needs to put more money in your pocket. No one is going to bring innovation to market unless there is an expected profit.
An innovative product or service has knowledge and know-how baked into it. One doesn’t need to be “super smart” to be innovative and bring a new or better product/service to market—simply smart within a single domain in which one excels.
The question then becomes, where does this knowledge and know-how come from? In broad strokes, knowledge and know-how can come from study (hence the notion of university spillovers) or come from aptitude and experience (hence the notion of learning by doing and apprenticeships). The latter we’ll call experience as a short cut. Clearly, there is great overlap in terms of study and experience driving innovation and the two reinforce and make each other stronger. The new measures presented by Goetz and Han are not the “same old same old” established metrics for innovation—e.g., the number of STEM degree graduates or patents in a region. Instead, they measure the relatively invisible relationships between industries, technologies and people.

Alfred Marshall was the economist who, early on, observed that similar industries located together to their mutual benefit. They shared similar workforce needs and often contributed to each other’s supply chain. Whether workers moved from firm to firm, or worker know-how was shared among friends down at the pub, worker know-how diffused throughout a region. Regions specialized.
A more recent contributor to this understanding about how and why many regions prosper is professor Michael Porter. (Porter’s cluster mapping project is also available via StatsAmerica.org.) As regions specialize, productivity, employment and profits increase. Encouraging industry cluster growth is an often-cited economic development strategy for regions to pursue.
As industrialization was taking hold, when one could buy a car that was any color at all as long as it was black, or there was one producer of jeans or one type of milk. Specialization made production more efficient. Over time, however, marketing and a customer focus began to eclipse production in terms of making products more differentiated and profitable. Or, if you will, products became more specialized.
The foregoing discussion about innovation presents a backdrop for the work of Goetz and Han. There are three key ideas. The first, industry input specialization, can be interpreted as the uniqueness of the input structure of the firm, industry or region as an aggregate of industries. The second, industry output specialization, can be understood as the uniqueness or specialization of the output structure for a particular industry—how many types of customers an industry sells to. Key idea one and two are rather like the recipe a restaurant uses to create a dish and the type of customers purchasing that dish. The more specialized in the ingredients, the more innovative on the input innovation side. The more targeted the customer consuming the dish is, or the more specialized the product or service, the more innovative on the output side. A taco food truck isn’t innovative because what it sells is rather generic—common. On the other hand, a Korean-fusion taco food truck may be innovative because it caters to a more narrow market niche.
The third key idea is the regional industry profile or evenness across different industries—how diverse or concentrated the industries in a region are. In our example, we are interested in the recipes and cuisine of a restaurant, but we are also interested in whether there is a super-abundance of restaurants or just a few. A cluster of exotic eateries in a region would have a high degree of employment concentration and would register as having a far greater proportion of employment than the national average. This industry cluster, likely part of a tourism cluster, would not be common across the national economic landscape. A counter example would be hairstylists or auto repair, which are typically based on local population and not unique.
In a similar way that a recipe book would describe all the needed ingredients and their proportions for a restaurant to transform those ingredients into delicious meals for their customers, so an input-output table describes the inputs a region requires to produce its output. Thus, the recipe book—with some cooking know-how—represents a large stock of knowledge for the restaurant. In a similar way, Goetz and Han utilize an input-output (I-O) table for a region as a stock of knowledge and a representation of industry structure and complexity.
The I-O table provides a description of industry input (“input innovation”) and output structures (“output innovation”). The I-O table helps to estimate the regional economic dark matter that describes innovation. The I-O table reports the input proportions of both products and services consumed in the production of an industry’s output.
The profile of employment head count by industry then allows one to estimate how evenly industries are distributed within a county. The Shannon Evenness Index (SEI)—also called an entropy index—provides a sense of how concentrated, or specialized, the industry structure of a county is. In our Indiana example below, we’ll see that Howard County had the lowest SEI for seven selected county scores for inputs because of its specialization/concentration in transportation equipment manufacturing.
While there are other important facets to the Goetz and Han analysis, we have enough for now to consider the dimensions of estimating much of the dark matter of innovation: the uniqueness or commonness of production inputs and outputs, and the specialization of a region’s industrial mix. Indeed, they cited Hidalgo and Hausmann (2009) who showed that more complex (or innovative) products are less common.
What values will these innovation dark matter scores take? One might expect that regions requiring unconventional inputs would have a higher value for innovation. This may be a result of high value-added specialized inputs (e.g., aircraft parts), or because the region is one of a few locations that refine oil, which requires specialized facilities to process. One might also find consumers of refinery products are also widespread—from airports to plastic feedstock to propane supply in rural areas to diesel fuel. Because the refinery products are not complex, or perhaps the consumers of refinery products are broad-based or common, the output innovation scores for petroleum products are lower.
Conversely, even though the input structure for business services are generic—office space, copy paper, desks and computers—the output may be very technical, sophisticated and specialized, so the output innovation score may be high.
Does innovation dark matter influence Indiana’s economic performance?
Figures 1 and 2 show the county-level input and output innovation values for Indiana using the downloadable scores available on the website of Northeast Regional Center for Rural Development at Pennsylvania State University.
The first easy-to-see difference between the two maps is that the output innovation map is darker, reflecting greater innovation content (and complexity) in the production of goods and services than in the input side of the production process. Without more digging, one can’t say for sure, but the implication is that Indiana’s producers consume lower value-added inputs and components and produce higher value-added products. Kosciusko County is a good specific example of this general observation. The county’s input innovation is negative while the output innovation value is positive. This innovation “split decision” is not rare across the state or across the county. That said, it does make one stop to consider the nature of production in a region and to what extent output consists of higher value-added, differentiated products and the degree to which a region is concentrated in common, or ubiquitous, products and services.
Figure 1: Dark matter input innovation scores
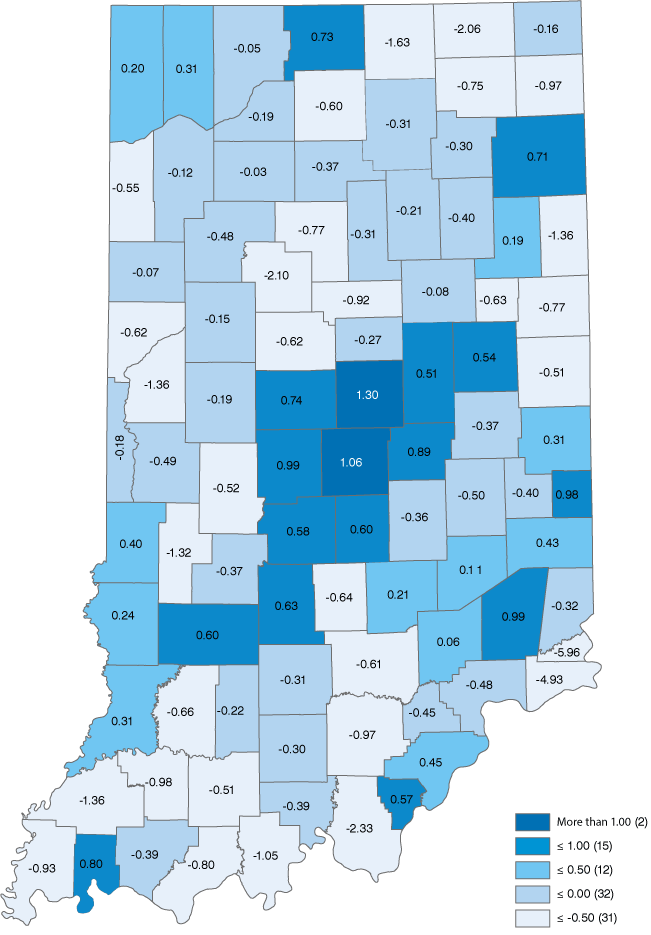
Source: IBRC, using data from the Northeast Regional Center for Rural Development at Pennsylvania State University
Figure 2: Dark matter output innovation scores
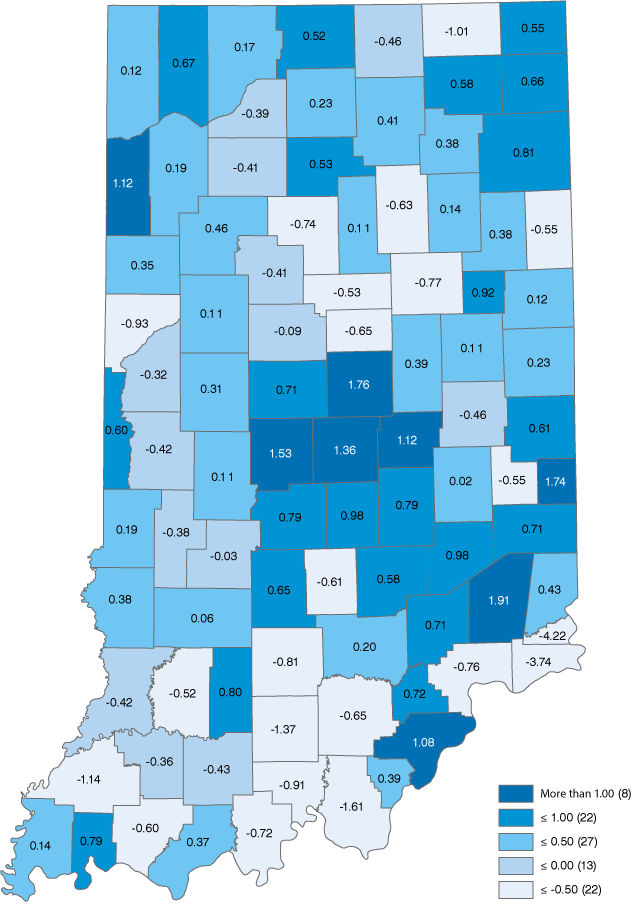
Source: IBRC, using data from the Northeast Regional Center for Rural Development at Pennsylvania State University
Table 1 presents the metrics for seven selected Indiana counties. The three measures are reported at the top so as to avoid the implication that the scores are directly based on values in the table.
Table 1: Innovation scores for inputs, outputs and industry diversity for selected counties together with the largest input purchase proportions for those counties
| Product or service input profile by 3-digit NAICS for selected Indiana counties | Allen | Bartholomew | Elkhart | Hamilton | Howard | St. Joseph | Washington |
|---|---|---|---|---|---|---|---|
| Innovation input dark matter score | 0.71 | 0.21 | -1.63 | 1.30 | -0.92 | 0.73 | -0.97 |
| Innovation output dark matter score | 0.81 | 0.58 | -0.46 | 1.76 | -0.53 | 0.52 | -0.65 |
| Shannon Evenness Index of industry diversity/specialization | 0.82 | 0.76 | 0.77 | 0.79 | 0.73 | 0.81 | 0.80 |
| Industry supplying inputs for county production | Allen | Bartholomew | Elkhart | Hamilton | Howard | St. Joseph | Washington |
| Chemical manufacturing | 0.04 | 0.03 | 0.06 | 0.02 | 0.02 | 0.05 | 0.07 |
| Primary metal manufacturing | 0.05 | 0.09 | 0.06 | 0.01 | 0.06 | 0.04 | 0.03 |
| Fabricated metal product manufacturing | 0.04 | 0.07 | 0.05 | 0.02 | 0.05 | 0.03 | 0.04 |
| Machinery manufacturing | 0.03 | 0.10 | 0.03 | 0.01 | 0.03 | 0.02 | 0.03 |
| Transportation equipment manufacturing | 0.16 | 0.12 | 0.23 | 0.01 | 0.31 | 0.09 | 0.11 |
| Wholesale trade | 0.06 | 0.09 | 0.08 | 0.04 | 0.07 | 0.06 | 0.07 |
| Insurance carriers and related | 0.05 | 0.01 | 0.01 | 0.12 | 0.02 | 0.04 | 0.02 |
| Real estate | 0.05 | 0.02 | 0.02 | 0.08 | 0.03 | 0.07 | 0.05 |
| Professional, scientific and technical services | 0.08 | 0.06 | 0.05 | 0.13 | 0.05 | 0.10 | 0.06 |
| Administrative support services | 0.04 | 0.02 | 0.02 | 0.06 | 0.02 | 0.04 | 0.03 |
Note: Blue cells indicate the top two 3-digit industries supplying inputs for county production.
Source: IBRC, using data from the Northeast Regional Center for Rural Development at Pennsylvania State University for the innovation scores, IBRC’s QCEW-Complete employment data for calculation of the Shannon Evenness Index, and IMPLAN’s Indiana-specific data for the industry input calculations.
These seven counties, like all of the counties in the state of Indiana, show a strong correlation between input and output innovation dark matter scores. Those with the higher input scores tend to have higher output innovation scores. The correlation between the input and output scores for the 92 counties in Indiana is 0.83. For the country as a whole, however, the correlation between county scores is lower, about 0.63. (This excludes all counties in Virginia because many geographic boundaries and definitions are not consistent with counties in the other 49 states and this can have pertinent effects on statistical analysis.)
The Shannon Evenness Index for the counties is a number that indicates how flat or spiky the column chart would be of industry employment proportions on the Y-axis and industries on the X-axis. The closer the SEI number gets to one, the more even (or less spiky). In Table 1, Howard County has the lowest SEI, indicating that its column graph of industry employment would be the most salient among the seven counties. Transportation equipment manufacturing would really stick out. For Howard County, about 31% of county inputs were from the transportation equipment manufacturing industry, the greatest proportion among the seven. As it happens, Howard and Elkhart counties had the greatest proportion of industry employment concentrations with 0.21 and 0.22 in that industry, respectively. The employment proportion values are not reported in a table for the sake of space, but mentioned as a reminder that the innovation dark matter doesn’t measure the regional employment mix but something akin to a regional production function. Innovation dark matter reports the knowledge embedded in the complexity and differentiation of production. The SEI measures the concentration/specialization or uniformity of industry employment.
Typically, economists and other social scientists assess the statistical relationship between a goal or desired outcome—a measure of performance like the growth in jobs or increases in earnings per job—with the variables of interest. Innovation dark matter scores are the variables of interest. The question is then: How much variation in employment—the variable that depends on measures of innovation—is explained by input and output innovation scores together with a measure of the level of specialization? The statistical measure for explained variation is called R-square. For our purposes, it is a measure of the explained variation in job growth with our innovation dark matter and energy measures. (It is customary to include other regional characteristics in assessing explained variation, but this is a high-level overview about dark energy and matter, not a peer-reviewed academic paper.)
Table 2 reports statistical analysis for counties in several Great Lakes states. Keeping in mind that the analysis reports unweighted scores for each state (county scores are not adjusted or weighted based on population or employment), one gets a sense that each state is different in terms of whether it is mostly an input innovation state or an output innovation state. The results for the 3,001 counties for the nation as a whole show that both input and output innovation, together with industry specialization or concentration, explain a modest variation in changes in employment. The value of 0.135 for the adjusted R-square shows a relatively high impact for these measures given that other regional characteristics were not included in this model. (Goetz and Han included additional variables, like educational attainment and population density, in their model.)
Table 2: Statistical results for input, output and industry diversity in selected Great Lakes states
| Geography | Explained variation, adjusted R-square | Input dark matter innovation score | Output dark matter innovation score | SEI industry diversity coefficient† | Observations (number of counties) |
|---|---|---|---|---|---|
| United StatesΩ | 0.135 | 0.001 | 0.006 | -0.073 | 3,001 |
| Indiana | 0.220 | 0.007 | - | - | 92 |
| Michigan | 0.148 | 0.009 | - | -0.126 | 83 |
| Minnesota | 0.195 | - | 0.007 | -0.061 | 87 |
| Ohio | 0.131 | - | 0.008 | - | 88 |
| Wisconsin | 0.205 | - | 0.007 | - | 72 |
† SEI negative values indicate greater specialization, lower industry diversity
Ω Excludes Virginia
Note: Values reported are statistically significant with p-values of 0.1 or less.
Source: IBRC, using data from the Northeast Regional Center for Rural Development at Pennsylvania State University
The results suggest that Indiana and Michigan industries innovate in the input dimension. The results for Minnesota, Ohio and Wisconsin suggest that industries in these states innovate in the output dimension. The results also suggest that the explained variation in employment growth in counties in Michigan and Minnesota is associated with specialization (or industry concentration) in those two states.
Given the heavy concentration of the auto sector in Michigan and Ohio, the input and output dark energy/matter scores are available in Figure 3. The reader is encouraged to review the county scores for these states to compare and contrast neighboring states and think about what may explain the innovation scores. Are the counties with high input scores also dominated by the auto sector? Are counties with high innovation output scores or with a large difference between input and output innovation specialized in other industries, such as life sciences or aerospace or consumer goods?
Figure 3: Dark matter innovation scores by state
Conclusion
This article started with the premise that measuring innovation is much like measuring dark energy and matter in the universe—difficult in the extreme. Researchers in regional science are advancing how we think about and measure innovation beyond simply counting patents. In this article, we briefly discussed what innovation is and then presented a distilled version of work recently published by Goetz and Han, highlighting how Indiana fares in pursuing innovation.
The key takeaways are:
- Unique inputs and complex industry processes suggest innovation.
- Differentiated and complex industry output suggests innovation.
- An industry that is present almost everywhere is not considered innovative.
- An industry (or an industry cluster) that is relatively rare and uncommon does suggest innovation.
Regional science is not yet finished in the pursuit to better conceptualize and measure innovation. Getting a correct read on small, rural counties and regions may present an ongoing challenge. Counties or regions that are dominated by one specialized industry, like mining or even hospitality and entertainment, e.g., Clark County, Nevada (Las Vegas), may present false positives or false negatives in terms of innovation. The more rural and less populated a region is, the more care one should take in interpreting the results.
So at the risk of distorting the work of Goetz and Han in our attempt to simplify and apply their measures to Indiana, and at the risk of potentially offending fellow Hoosiers who can make a justifiable claim that their firm or industry or county is innovative, we presented these new measures. Within the next few months, StatsAmerica.org will make several of these measures available to the public with our new Innovation Intelligence—the next step in measuring and reporting regional innovation following on the success of the Innovation Index 2.0. We welcome your feedback to make our measures better.
References
- Goetz, S. J., & Han, Y. (2020). Latent innovation in local economies. Research Policy, 49(2), 103909.
- Hidalgo, C. A., & Hausmann, R. (2009). The building blocks of economic complexity. Proceedings of the National Academy of Sciences of the United States of America, 106(26), 10570–10575.
- Marshall, A. (1966). Principles of economics (8th ed.). London: Macmillan.
- Porter, M. E. (2003). The economic performance of regions. Regional Studies, 37(6-7), 549–578.



