
How networks matter in economic development: Interdependence among industries, occupations and labor force skills
Measuring the dark matter & energy driving regional economic performance, part 2
Co-Director, Indiana Business Research Center, Indiana University Kelley School of Business
In an earlier IBR piece, we presented recent research on how to measure the invisible forces, only indirectly observable, that drive innovation.1 In this article, we explore another dimension of economic performance that only recently has come to be recognized: the invisible interdependencies among industries, occupations and labor force skills. In short, the presence of (invisible) linkages among people and entities that inhabit a region.
In this article, we compress cutting-edge research conducted by a research professor at the School of Complex Adaptive Systems at Arizona State University and a newly minted Ph.D. from the Schar School of Policy and Government at George Mason University, with whom the IBRC had the pleasure to work on a project designed to explore unconventional ways to understand and measure local, regional and state economic development. In other words, the research presented below is not my own but that of project research partners Shutters and Waters and the “we” that follows refers to the three of us.2
There are so many key takeaways, we list them as an executive summary and expand upon them in the body of the article:
- Tightness is the big idea. It is a measure of invisible interdependencies within the regional economic landscape.
- A tightness score (T-score) is the metric for the interdependencies of regional industries, occupations and labor force skills.
- Tightness is derived from a type of network analysis and complex adaptive systems approach to understanding the nodes and linkages (or edges in the parlance of networks) between the nodes.
- The nodes are comprised of either industries, occupations, or the skills and occupational characteristics of the labor force.
- The concentration, density or regional specializations of the linkages—the T-scores—provide insights into regional economies.
- The T-scores explain a non-trivial portion of the economic performance differences among regions.
- The T-scores are also shown to relate to several regional characteristics, such as the presence and concentration of certain types of industry clusters—like business services and finance—as well as the dependency upon external sources of income and regional educational attainment.
- Interpreting the tightness of regions has its challenges. This leads to asking questions that start with “why.” The data and the questions will enlighten policymakers and economic development practitioners as to the latent structure of a region’s economy.
- Generating and raising questions about what drives economic performance is the motivation to conduct the research about tightness.
- The by-products of the tightness analysis can help inform policy directions about transitioning workers from one type of job (that may be shrinking in economic importance) to another type of occupation that better aligns with workers’ skills and is in greater demand now and in the future.
- Indiana has several counties that rank well in terms of T-scores among the broader Great Lakes states.
- There is a positive statistical association between T-scores and performance measures, such as job growth and productivity (measured by GDP per worker) growth.
- With tightness comes efficiency and productivity, but also fragility and lower economic resilience.
- Increasing tightness has been shown to be statistically associated with higher economic growth but negatively associated with resilience to economic shocks, such as the Great Recession.
- Tightness may also help to explain the labor market effects of COVID-19 given that it helps identify the structural elements of labor market and income fragility.
This article is based on five research papers—a couple published and a couple not yet—that are cited and linked in the references. This research summary is structured as follows. First, we explain the motivation for presenting this material. Second, we describe the interdependence concept—tightness—its strengths and weaknesses and highlight the methods used to describe and measure the interconnectedness between each analytical category type—industry, occupation and skills. Third, tightness is placed in a network analysis framework. Following that, we present maps of Indiana and the Great Lakes region showing tightness scores by county. Fifth, we present the empirical results and statistical associations between tightness and measures of economic performance, especially for Indiana and the Great Lakes region. We conclude with several questions, a couple of answers, and several additional suggestions for applying the concept of tightness and conducting additional research.
Motivation
A perennial question in regional economic development is: What drives economic performance (which can be measured by job creation or productivity or rising income and living standards)? A more recent salient question arose from the ashes of the Great Recession and, more recently, due to the COVID-19 pandemic and natural disasters: What is resilience and how do we build it? (For purposes of this article, we define resilience as a regional economy’s capacity to withstand and/or recover from an economic shock.)
Answers to these questions have been largely about regional characteristics for which there are readily available data from official government statistical agencies like the U.S. Bureau of Labor Statistics, the Bureau of Economic Analysis, the Department of Education and the Census Bureau, among others. These data are relatively easily conceptualized, measured and accessed.
As with latent innovation or economic “dark matter” discussed in our earlier article, there are invisible relationships that can be teased out of the official data. In the case of latent innovation, one can tease out the degree of regional complexity and specialization associated with production. In the case of tightness—which we introduce here as an aggregate measure of interdependences—one can tease out relationships that exist between pairs of, say, industries or occupations. These relationships are based on two dimensions: 1) the similarity (or dissimilarity) of the entities like industries or occupations and 2) the geographic concentration or density of a pair of the entities that co-locate within a region. The operating assumption is that when a concentrated pair of industries inhabit or are co-located in a region (in our case, county), that implies that those two industries are somehow related.
Similarity and co-location tells us much about the economic structure and the performance and resilience of a region.
What is tightness?
Regional economies are complex adaptive systems. The analytical framework we take is one from ecology: If two species inhabit the same landscape, they are somehow related. If the two species rise and fall in tandem—if the demise of one species is correlated with the decline in the health or presence of another—that is a dead ringer for species relatedness, even if neither one is on the other’s typical dinner menu.
So the tightness concept takes its form by employing ecological techniques of co‐occurrence analysis to infer interactions. In our case, those interactions are between industries, skills and occupations. We then create an aggregate measure of economic tightness, capturing the degree of integration or interconnectedness among a region’s industries/skills/occupations. Spoiler alert: Industry tightness is positively correlated with a region’s economic productivity but negatively correlated with one definition of resilience—bounce-back or a region’s recovery to pre-shock employment and productivity following a shock. This is why the concept and measure are important.
A pair of two industries may be related because they are both links in a supply chain, for example, from foundries to forging to auto parts to auto assembly. The industries may be related because they are both needed in combination with each other for a specific production activity, for example, the robotics hardware and the systems integration that create a seamless assembly line. This type of relatedness is captured in the production-based NAICS classification system. But relatedness (or interdependence) isn’t just about common classification schemes. Industries, outside of production input structures, may be related because the workers or clients of a regional anchor industry—for example, a university or hospital—want specific goods and services. So bicycle shops, electronic scooters and bars provide the services that college students spend their money on. The bicycle shops and bars share a customer base anchored by a university. In a similar fashion, hotels and restaurants spring up around military bases.
For instance, from Shutters and Waters (2020b), the industry pair with the highest relatedness score is motion picture and video industries (NAICS 5121) and agents and managers for public figures (NAICS 7114). This pair of 4-digit NAICS logically and empirically co-occur in the same location. The industry pair that share the lowest industry relatedness score is cut and sew apparel manufacturing (NAICS 3152) and space research and technology (NAICS 9271). The observation that hand-made apparel manufacturing and space research rarely co-occur in the same location also passes the smell test. These two extremes are easy to interpret, but the more difficult interpretations are in the middle of the T-score spectrum when, on one hand, there may be supply chain interdependencies but there may be non-obvious co-occurrences that require additional thought about the interdependencies.
There may be occupation pairs that tend to co-locate in a concentrated fashion as well. An interesting thought experiment may be: What occupations would congregate around the creative class? Perhaps personal trainers, baristas, dog walkers or Uber/Lyft drivers to give a couple of suggestions. The spending habits of the creative class would beget the entry of new businesses and the occupations associated with those new businesses to fulfill the creative class consumption profile. In other words, it isn’t just an industry input structure—supply chain—that matters, but the consumption patterns of the occupations (i.e., what the workers spend their money on).
Regional occupation dynamics—or to put it more starkly, the feast-famine cycle—tend to follow industry dynamics, but with some caveats. The occupational profile of a region is affected by local/regional spending as well as its industry profile. Occupations influence income stratification and, maybe more important in our times, holders of wealth. That wealth, be it stock market or real estate, can serve as a buffer and an economic shock may not influence that upper strata’s spending patterns in the same fashion as blue-collar workers or the non-tech rank and file. College students, many if not most attending on mom and dad’s dime, may not adjust their spending significantly during an economic shock. One would not expect as large a spending swing, or changes in hospitality or personal services employment, due to an economic shock for those regions with larger incomes and wealth. But it depends on the type of economic shock. (We broach the effects of the COVID-19 pandemic in a concluding section.)
Finally, labor force skill pairs also tend to concentrate geographically. The skills dimension may be the more difficult to interpret because many skills—as defined by the U.S. Bureau of Labor Statistics and associated organizations focused on the labor market—that are in high concentration are also ubiquitous across a majority of occupations. These are the so-called soft skills. As a result, soft skills (like cooperating with others, resolving conflict, active listening, oral expression and observing critically), among other non-technical or knowledge-based skills, will not differentiate between occupations well. Soft skills, such as empathy, are required for brain surgeons as well as hotel receptionists.
As noted above, the tightness scoring method addresses these phenomena by how close or similar (or proximate) any two occupations are—brain surgeons and hotel receptions would be relatively dissimilar. The T-score also measures the relative regional concentration of that occupation pair. One might think of the method as pointing to occupation pairs as complements (brain surgeons and operating room nurses) or substitutes (pediatricians and nurse practitioners). The method also points to the concentration of those pairs and, in the regional aggregate T-score, the degree to which they are interdependent.
An example may help. In order to determine the skill sets of an occupation, Shutters and Waters (2020a) used job characteristics data from O*NET, more specifically, the “individual work activities” (IWA) associated with a job. There are some 322 IWAs at the time of this writing (although O*NET seems to constantly revamp their definitions and thereby keep the users of their data off balance). These IWAs can be viewed as similar or dissimilar across a spectrum. Waters and Shutters provide a ranking of the independence of IWA pairs. The highest, or most interdependent work activities, are “the study of details of artistic productions” paired with “altering audio or video recordings.” The lowest IWA pair is “evaluating scholarly work” and “hunting animals.” Again, the scores of these pairings pass the smell test at the ends of the T-score spectrum. Industry and occupation concentrations (or regional specializations), together with skills density, are estimated using location quotients.
The foregoing provides evidence that the tightness and T-score methods are a robust, if a partial, means to understanding many of the invisible connections and interdependences between economic agents, entities and characteristics. Many highly interdependent pairs of the T-score variety are seemingly unrelated in a production or NAICS category sense. The interdependence of tightness also operationalizes the sort of industry relatedness ascribed to industry clusters and the positive externalities first identified by Alfred Marshall (1966) and made popular with the Cluster Mapping Project. These industries are interdependent because they share specialized labor skills, benefit from knowledge spillovers, have a mutual, streamlined supply chain, market to similar customers, etc. And it just so happens they also tend to share the same geographic space.
We hope that in our descriptions above, we have provided just the right level of detail and depth for the reader to understand what tightness measures are and how they are constructed. There is, however, one more salient aspect of the tightness analytical framework: Tightness is another word for network.
Tightness is another word for network linkages
Those familiar with network analysis and complex systems were likely interpreting the above descriptions in a network frame. Indeed, in a network visualization, the nodes are the occupations or industries and the interdependences are the linkages (or edges) between the nodes. These tightness scores by region can be graphed and compared and contrasted to understand strengths, weaknesses and vulnerabilities of a region’s economic ecosystem.
Figure 1 provides a visualization of how the pairing translates to T-scores and how those T-scores can be expressed in graphical space. The figure shows how the T-scores take into consideration the similarity of all pairs taken together and projects those similarity relationships in a picture. And from that picture, we can see how close or distant various nodes are.
Figure 1: Visualizing Tightness-scores
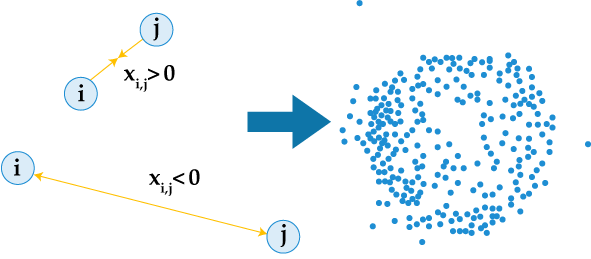
Note: Industries that tend to co-occur together in regions have x > 0 and will tend to be closer to each other in the final network. Industries that rarely occur together will have x ~ 0 or x < 0 and will be pushed apart in the final network. Each node represents a 3-digit industry and, while the placement of nodes is generally arbitrary, the distance between any two nodes is a function of an industry’s interdependence x with all other industries. Links between nodes have been removed for visual clarity.
Source: IBRC, based on a graphic originally published in IAB Discussion Paper: “Industry interconnectedness and regional economic growth in Germany”
Figure 2 presents examples of three metropolitan statistical areas (MSAs). The nodes are skills and proximity between skills is a function of pairwise interdependencies. All linkages/edges greater than zero are displayed. Node presence is determined using a “community detection algorithm.” For the element-based skills network, the location of the nodes are clustered between sensory-physical skills at the top and socio-cognitive skills toward the bottom of the graphic.
The linkages or edges between the nodes—the skills—are constant, and of a more subtle shading, for all three. The dots or nodes are shaded based on their relative concentration in Indianapolis, Chicago and Seattle. The T-scores for the three cities are also presented and show that the more tangible or physical skills in Indianapolis congregate in the upper portion of the graph while the technical and cognitive skills are dominant in Seattle in the lower portion of the graph. Chicago presents more evenly distributed skills nodes.
Figure 2: Skill networks—interdependences—and concentration for three metropolitan statistical areas
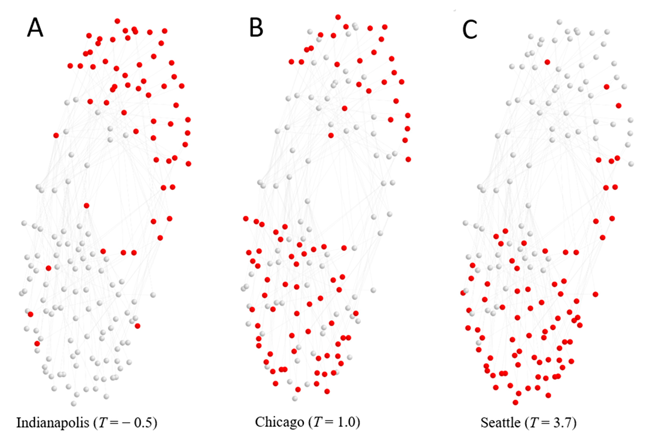
Note: (A) Indianapolis is largely within the sensory-physical cluster, while (B) Chicago is more balanced across lobes and (C) Seattle is located almost exclusively within the socio-cognitive cluster of skills. Normalized tightness scores of each city are shown in parentheses.
Source: Originally published in Shutters, S. T., & Waters, K. (2020a). Inferring networks of interdependent labor skills to illuminate urban economic structure. Entropy, 22(10), 1078. Retrieved from https://doi.org/10.3390/e22101078 (Licensed under Creative Commons CC BY 4.0.)
That there are these non-obvious dependences based on the T-scores may be the genius behind tightness because it raises many questions that start with “why.” Figuring out the “why” may then inform policy initiatives—industry retention and attraction, for example—and can cast light on sectors that may be resilient or, in contrast, fragile. That greater tightness has been found to increase efficiency and productivity may make sense given the argument for industry clusters spurring competitiveness. It may also make sense that greater tightness makes the overall regional economic ecosystem more fragile—less resilient—because when one industry suffers a blow, other close proximity nodes (industries) suffer too. As the old adage goes, when one big industry catches a cold, smaller dependent industries catch the flu.
Tightness and performance
The co-authors Shutters and Waters assessed the empirical and policy significance of tightness. One use of this technique is that the level of interconnectedness within an economy’s workforce, or its economic tightness, is positively correlated with more severe declines in economic performance following a shock. This outcome aligns with the purported Panarchy theory of complex systems, which hypothesizes that systems with greater connectedness—or tightness—are more efficient. But they are also more brittle and less able to absorb and adjust to shocks. Thus, economic tightness is intimately linked to fragility and resilience.
As one takes a brief look at the relationships between tightness and other regional characteristics, some regional characteristics appear to emerge. The overview that follows may not do justice to the research and analysis of Shutters and Waters; therefore, we encourage you to read the papers to get finer detail on the precise statistical relationships.
As presented above, there are three types of tightness: skills, occupations and industries. While we present T-scores by county to provide maps in more stark relief, the better analytical geographic boundary is a labor market or commuting region, such as a metropolitan statistical area (MSA). MSAs typically have a central core city. (But not always. Los Angeles has several dense urban cores within one county.) MSAs and the larger geographic boundary of a labor market area have greater populations and a more diverse set of industries and occupations and, therefore, a broader array of industry or occupation pairs that co-locate. Unless stated otherwise, the summary of the research results presented below are based on an MSA unit of analysis.
The relationship between skills tightness and economic productivity were compared to a region’s per capita GDP and per capita personal income. Both were significantly and positively correlated with skills tightness. Skills, in this case, were defined using O*NET data for both occupation characteristics—for example, technology skills, tools used, knowledge, abilities, education level and work styles. Skills were also complemented by individual work activities (IWA mentioned above). The relationship between tightness and per capita GDP remained positive and statistically significant irrespective of MSA scale/size. Per capita personal income was also significant and positively correlated with both occupation characteristics and IWA-based tightness. These statistical associations for skills-based T-scores corroborate with earlier research calculating MSA occupation-based interdependence values.
Both skills-based tightness and the previously published occupation-based tightness are associated with higher economic productivity.
That said, in terms of resilience, skills-based and occupation-based measures differ in their relationship to a response to a shock. Occupation-based tightness is negatively correlated with an MSA’s change in GDP during the 2007–2009 recession. Skills-based tightness is positively correlated with change in GDP during the Great Recession. The question then becomes: How do we explain the difference between the two?
One plausible explanation depends on the ecological concepts of species niches and competitive exclusion. Occupations are, metaphorically, species in an economic ecosystem. Occupation pairs with low interdependence—x less than zero in Figure 1—share similar economic roles that have limited space (or niches) within an ecosystem. In other words, these two occupations are likely competitors because they perform a similar function and are likely to have similar skill sets. For example, industrial engineer and petroleum engineer have a strong negative interdependence; they don’t tend to co-locate. But they also have in common many key O*Net skills like systems analysis, programming and complex problem solving, which are highly interdependent.
Skills-based tightness and occupation-based tightness have opposite correlations with GDP growth following a shock. This suggests that there is a trade-off between labor structures that enable resilience and those that foster productivity. This trade-off can be viewed much like the first graph presented in your Economics 101 class—the curve that plotted the trade-off between “guns and roses.” To get more roses, you must give up some guns. (Okay, maybe it was between guns and butter, but roses are more fun, don’t you think?)
The trade-off phenomenon may be more easily grasped by considering industry tightness.
In another paper focusing on industry tightness, Shutters and Waters (2020b) found a trade-off between productivity and resilience. In order to have a high industry interdependence, two industries have to be regionally specialized—that is, the industry pair are rarely concentrated in other regions, rather like hardwood products and furniture manufacturing—because it is likely the case then that they are more efficient and productive located together than with geographic separation.
The correlation between the average score of industry‐pairs that co‐occur within the MSA and the MSA’s per capita GDP is negative and statistically significant. Regions with industries that rarely co‐occur are more productive than regions with more co‐occurring industries that are widespread across regions. This provides additional evidence that the co‐occurrence measure at the MSA level signals the inter‐industry productivity benefits of industry proximity that are not captured by the traditional diagnostic measures and tools (such as location quotients). MSAs with less ubiquitous industry pairs are more productive. This corroborates past research on economic structures driving regional performance.
Synthesizing the results of this study on industry tightness with previous work using tightness based on occupations and on skills, Shutters and Waters find that industry tightness is linearly correlated with occupational tightness, while the relationship with skills tightness is non‐linear. In sum, industrial and occupational tightness appear to be closely related. On the other hand, skills tightness appears distinct from the other two measures at the MSA geographic unit of analysis (and these relationships also hold at the county level across the Great Lakes region).
This section was planned to be brief—but wait, there’s more. Waters and Shutters also applied these frameworks from rural places to populous regions (2021b). Using the performance measure of gross domestic product (GDP), earnings by place of work and employment change, they found that the effect of tightness on economic output (GDP) is only modestly influenced by regional population size. Intriguingly, the most rural and most urban regions have the highest share of their specialty skills in the socio-cognitive lobe of the skills-space. Given that skills tightness is positively correlated with economic output, that rural regions may have a structural, skills-tightness advantage is encouraging. What accounts for this? Higher tightness scores appear to be a function of teaching and training skills concentration in rural regions, the researchers have tentatively found.
Economic productivity, both skills tightness and industry tightness, are positively and significantly correlated with both log of GDP per capita and log of workplace earnings, with the larger geographic units of labor market areas (that are geographically larger than MSAs) and combined statistical areas generally having stronger correlations. Overall, the correlations between both tightness measures and population vary notably when the geographic unit is altered. That said, correlations between tightness and economic output are relatively stable. The fact that correlations between tightness and log GDP per capita are more stable than tightness and population between geographic levels suggests that the correlation between tightness and economic output is robust.
Finally, as we have shown, the tightness measures and performance have a sufficient statistical relationship that warrants further study and many more why questions for policymakers, site selectors and economic development practitioners. For example, what drives the industry, occupation and skills scores? Industry structure? Education level? The dependence of the region’s employment upon producing for “export” versus serving the local population? (Export is another term for traded industries.)
Mapping tightness across Indiana and the Great Lakes
We present the T-scores for industry, skills and occupations by county to put the differences by county in greater relief, and to encourage questions about why counties that may have considerably different economic foundations may share higher (or lower) tightness scores. As we presented above, a region may have one type of tightness such as skill interdependences, but not other industry or occupation interdependencies. It is very likely that Bartholomew, Elkhart and Gibson counties, with their automotive and industrial machinery supply chains, have a high degree of industry tightness. Kosciusko and Whitley counties likely have the industry co-location associated with medical devices. Monroe and Tippecanoe counties likely share the pairing of the university anchor and student-consumption patterns, even if those pairings are not related to supply chain interdependencies.
The “why” questions proliferate as we move to other types of similarity and concentration. Along the skills dimension, Hamilton County, Indiana, registers the greatest skills tightness score—which makes one wonder about how rare and concentrated certain occupations are in that county. Note: These are jobs counted in Hamilton County at the firm level (not commuter jobs of engineers who live in Noblesville but work in Kokomo or accountants who work in downtown Indianapolis). In the same way, the scores for Martin, Marion and Monroe counties likely tell a tale. The greater T-score for Martin may be driven by the close collaboration of engineers at Crane NSWC, while Marion’s score may be the accountants, lawyers and consultants who share many skill sets and inhabit the same business services ecosystem. Monroe County’s T-score may be an artifact of both university employee skill-set concentration as well as skill-set complementarity in the medical device production process.
We hope that the Indiana and Great Lakes region maps and tables will encourage the reader to explore the possible explanations for the scores. Several counties in the “Top 15” have similar scores. Why would Ann Arbor (Washtenaw County) have industry, occupation and skills tightness scores so similar to Minneapolis (Hennepin County)? Why would the Michigan counties of Antrim, Clare, Gladwin, Manistee, Missaukee, Tuscola and Van Buren all have similar T-score profiles—low scoring in the industry and skills dimensions, but in the top 15 county scores among the 524 Great Lakes counties in terms of occupations?
Again, our assignment isn’t providing answers. It is about asking great questions and providing the data and tools to help answer great questions. We hope that the following maps showing T-scores by industry, skills and occupations will help the reader and researchers together develop better questions about their region.
Figure 3 presents the Indiana industry, skills and occupation T-scores by county.
Figure 3: T-scores for Indiana counties
Figures 4, 5 and 6 present the Great Lakes states industry, skills and occupation T-scores by county.
Figure 4: Industry T-scores for the Great Lakes region
Figure 5: Skill T-scores for the Great Lakes region
Figure 6: Occupation T-scores for the Great Lakes region
Table 1 reports the top 15 T-scores for Indiana counties, with the top 15 counties emphasized by shading and bold text for a particular tightness score.
Table 1: Top 15 T-scores for Indiana counties
| County name | Skill | Occupation | Industry |
|---|---|---|---|
| Bartholomew | -0.52 | -3.03 | 2.69 |
| Brown | -0.06 | 0.15 | 0.02 |
| Clinton | -0.18 | -0.80 | 0.26 |
| Crawford | -0.55 | 0.62 | -0.64 |
| Daviess | -0.18 | 0.28 | -0.42 |
| Decatur | -0.57 | -1.65 | 1.36 |
| DeKalb | -0.33 | -2.40 | 1.63 |
| Delaware | 0.13 | 0.29 | 0.24 |
| Elkhart | -0.48 | -2.43 | 1.94 |
| Franklin | -0.87 | 0.64 | -0.37 |
| Gibson | -0.62 | -1.34 | 2.58 |
| Greene | -0.74 | 0.69 | -0.49 |
| Hamilton | 3.18 | -3.81 | 0.98 |
| Harrison | -0.36 | 0.74 | -0.40 |
| Hendricks | -0.38 | -0.19 | 1.35 |
| Jackson | -0.39 | -3.01 | 1.20 |
| Jennings | -0.16 | 0.06 | 0.30 |
| Knox | -0.82 | 0.69 | -0.47 |
| Kosciusko | -0.35 | -1.83 | 0.92 |
| Marion | 0.51 | -2.11 | 1.21 |
| Martin | 1.06 | -3.02 | 0.58 |
| Miami | -0.27 | 0.65 | -0.46 |
| Monroe | 1.92 | 0.51 | 1.53 |
| Montgomery | -0.15 | -2.44 | 0.76 |
| Morgan | -0.30 | 0.62 | -0.31 |
| Newton | -0.42 | 0.69 | -0.40 |
| Noble | -0.37 | -2.72 | 1.14 |
| Parke | -0.45 | 0.61 | -0.52 |
| Pike | -0.60 | 0.66 | -0.58 |
| Porter | -0.32 | 0.57 | 0.13 |
| Randolph | -0.21 | 0.56 | -0.23 |
| Shelby | -0.16 | 0.01 | 0.51 |
| Spencer | -0.22 | 0.61 | -0.33 |
| St. Joseph | 0.61 | 0.40 | 0.41 |
| Starke | -0.80 | 0.59 | -0.35 |
| Steuben | -0.15 | -0.13 | 1.31 |
| Sullivan | -0.26 | 0.65 | -0.48 |
| Tippecanoe | -0.51 | 0.43 | 1.42 |
| Tipton | -0.20 | -0.25 | -0.03 |
| Washington | -0.16 | 0.37 | -0.22 |
| Whitley | -0.33 | -1.88 | 0.90 |
Note: Bold text and shading represent a top 15 ranking for each particular tightness score (e.g., skill T-scores) among all Indiana counties (N=92).
Source: IBRC, using data from Shutters and Waters
Table 2 reports the top 15 county T-scores for the Great Lakes states, with the top 15 counties in the six-state region for a particular tightness score shaded and bold.
Table 2: Top 15 T-scores for the Great Lakes region
| County | State | Skill | Occupation | Industry |
|---|---|---|---|---|
| DeKalb | IL | -0.70 | 0.71 | 0.02 |
| Henderson | IL | 2.48 | 0.33 | -0.44 |
| Logan | IL | -0.77 | 0.70 | -0.39 |
| McLean | IL | 2.09 | -3.56 | 1.48 |
| Mercer | IL | -0.73 | 0.72 | -0.56 |
| Will | IL | -0.42 | 0.72 | 0.02 |
| Bartholomew | IN | -0.52 | -3.03 | 2.69 |
| DeKalb | IN | -0.33 | -2.40 | 1.63 |
| Elkhart | IN | -0.48 | -2.43 | 1.94 |
| Gibson | IN | -0.62 | -1.34 | 2.58 |
| Hamilton | IN | 3.18 | -3.81 | 0.98 |
| Harrison | IN | -0.36 | 0.74 | -0.40 |
| Monroe | IN | 1.92 | 0.51 | 1.53 |
| Tippecanoe | IN | -0.51 | 0.43 | 1.42 |
| Antrim | MI | -0.62 | 0.70 | -0.05 |
| Clare | MI | -0.69 | 0.75 | -0.23 |
| Gladwin | MI | -0.27 | 0.71 | -0.24 |
| Ingham | MI | 2.44 | 0.13 | 0.20 |
| Manistee | MI | -0.62 | 0.71 | -0.45 |
| Missaukee | MI | -0.17 | 0.70 | -0.49 |
| Oakland | MI | 2.65 | -2.13 | 1.27 |
| Tuscola | MI | -0.43 | 0.74 | -0.43 |
| Van Buren | MI | -0.46 | 0.72 | -0.33 |
| Washtenaw | MI | 2.50 | -1.34 | 1.97 |
| Hennepin | MN | 2.53 | -4.43 | 1.65 |
| Lac qui Parle | MN | -0.81 | 0.71 | -0.47 |
| Mahnomen | MN | 2.60 | 0.10 | -0.58 |
| Norman | MN | 2.67 | 0.18 | -0.51 |
| Olmsted | MN | 1.91 | -7.50 | 1.69 |
| Rock | MN | 2.69 | -1.24 | -0.30 |
| Delaware | OH | 2.47 | -4.21 | 1.13 |
| Franklin | OH | 2.32 | -1.37 | 1.39 |
| Gallia | OH | 2.37 | -0.11 | -0.16 |
| Greene | OH | 2.48 | -0.72 | 1.69 |
| Hamilton | OH | 2.37 | -2.13 | 0.81 |
| Montgomery | OH | 2.98 | -1.28 | 0.69 |
| Shelby | OH | -0.37 | -1.51 | 2.04 |
| Union | OH | -0.45 | -2.27 | 1.88 |
| Douglas | WI | -0.26 | 0.75 | -0.40 |
| Milwaukee | WI | 2.37 | -0.89 | 0.70 |
| Pierce | WI | -0.85 | 0.72 | -0.20 |
| Sheboygan | WI | -0.28 | -1.74 | 1.56 |
Note: Bold text and shading represent a top 15 ranking for each particular tightness score (e.g., skill T-scores) among all Great Lakes counties (N=524).
Source: IBRC, using data from Shutters and Waters
Analyzing the Great Lakes region
What follows is a statistical assessment for the 524 counties in the Great Lakes states. These states share many similarities, allowing for more appropriate comparisons than the entire 50 states.
In terms of job growth, the most compelling variables (or characteristics)—those that survived statistical robustness checks—are presented below based on relationship to employment growth.
Positive effect
- Industry T-score
- Occupation T-score
- Percent of population ages 25 and older with a bachelor’s degree
- Dependency of households upon government income programs (positive coefficient means less dependent)
- Share of local industries serving population (in contrast to traded/export-to-other-regions)
Negative effect
- Skill T-score
If instead total patent count—a proxy for innovation—by county is the performance measure, the following relationships hold for the “four explanatory variable” model:
Positive effect
- Skill T-score
- Occupation T-score
- Business services cluster employment proportion
- Finance and banking service cluster employment proportion
We also dipped our toes in assessing the relationship between patenting and tightness. In another regression model—total patents as the dependent variable—that also included variables for scale (total employment) and educational achievement (percent with a bachelor’s degree) both typical control variables and business services were positive and statistically significant. Finance and banking in the “full model,” however, was not.
The explained variation in the objective variable—total patent count in 2018 by county—for the four-explanatory-variable-model is a high 0.75 r-squared. Given that the business services cluster percent of employment (or cluster proportion) has expanded so greatly over the last two decades, it is not surprising that it has an out-sized effect on both general patent production and job growth. Using only the 524 counties of the Great Lakes region may play a role in these results because the region overall isn’t a patent powerhouse like Silicon Valley with tens of thousands of patent awards across a wide range of technology types. Rather, across many technology types, the region has both a modest and well-distributed number of patents.
Industry tightness in the Great Lakes states can be statistically explained by total employment, percent with a bachelor’s degree, share of local industries (the only negative relationship) and proportions of the following clusters: auto manufacturing, business services, distribution and electronic commerce, education (primary through tertiary), furniture and production technology and equipment, which all have positive and significant coefficients.
Occupational scores for the region are interesting but not surprising. Scale and educational level are positive like industry with similar coefficients. As with industry T-scores, local share has a negative coefficient. The other explanatory variable coefficients (with significance statistically) resemble the industry tightness both positive and negative. The share of education employment, however, is negative, in contrast to both industry and skill coefficients which are positive and statistically significant. This may be an artifact of how dissimilarity is measured between industries, skills and occupations. Occupation titles and knowledge bases are distinct and different across the university departments even though it is in one industry, the university industry. The dominant skills for university faculty and staff are defined by abilities in student instruction and similar work activities. Knowledge bases that differentiate physics professors from language professors are occupational characteristics.
Questions and potential applications for tightness
In the late nineteenth century, Alfred Marshall asked an important question about why industries that are related based on labor force skills and production inputs inhabit the same geographic space. The upshot today is that we have an evolving understanding and measurement of industry clusters as a driver for regional competitiveness and the benefits of industry co-location. The recent body of work of Shutters and Waters expands the knowledge frontier of what contributes to the agglomeration economies that reinforce competitiveness—namely the network relationships baked into the tightness concept. For example, industry tightness may encourage economic activity to become more productive by leveraging the complex interactions of a tightly linked economy to find more market and production opportunities for existing regional industries. There may be a drawback, however, in an ecological sense. A type of crowding out of industries—species as a metaphor—may arise as the symmetry among industries is overrun by a handful of dominant enterprises.
Applying a complex systems approach and a network analysis framework to regional industry dependencies will help to both understand the invisible factors that drive cluster development, but also identify possible maladaptive processes before doing extensive damage to the health of a regional economy.
In this article, we presented the question, and answer, to whether higher degrees of interdependencies among industries, skills and occupations increase efficiency and/or resilience—yes to efficiency and no to resilience to economic shocks such as the Great Recession.
Shutters and Waters (with additional authors) would also make the case that the concept of tightness will be useful for evaluating the economic fallout of COVID-19 (Shutters et al., 2021). Economic output dropped by about 5.0 percent in Germany during the Great Recession and again due to COVID-19. They suggest a comparison of the two shocks using the tightness concept and measure. The job losses were much different between the two events. They suggest that the Great Recession was much more devastating to particular industries in contrast to the more recent COVID-19 job losses that were much more evenly spread across regions and across industries.
Having the natural experiment of COVID-19’s effect on the economy would help to pressure test the notion that tightness increases fragility and reduces resilience.
No doubt that additional inquiries, region by region, could assess whether tightness is an attractive magnetic force for foreign direct investment. Or, if tightness is dissolving over time in a region, that may presage closures and a downward economic spiral.
Conclusion
In this article, we introduced the concepts of interdependencies only recently unveiled among economic agents and entities in a regional economy. Regional economies are complex adaptive systems and the approach of a couple of colleagues, Shade Shutters and Keith Waters, helps to tease out relationships among industries, skills and occupations that heretofore have not been considered in our understanding of agglomeration economies, industry clusters and regional economic dynamics. Moreover, we have seen that these interdependencies contribute to efficiency and productivity, but also tend to reduce resilience to economic shocks. The research and learning is still in the early stages. As researchers learn more about networks and tightness, we expect to gain a more complete comprehension of the drivers of economic growth and policy applications that can accelerate economic well-being.
Notes
- Slaper, T. (2021, Spring). The dark energy and matter that drives economic performance. Indiana Business Review. www.ibrc.indiana.edu/ibr/2021/spring/article2.html
- See the References section for the papers and research. Tightness scores by county were independently generated and provided by Shutters and Waters.
References
- Marshall, A. (1966). Principles of economics (8th ed.). London: Macmillan.
- Shutters, S. T., Seibert, H., Alm, B., & Waters, K. (2021). Industry interconnectedness and regional economic growth in Germany. IAB-Discussion Paper (No. 7/2021).
- Shutters, S. T., & Waters, K. (2020a). Inferring networks of interdependent labor skills to illuminate urban economic structure. Entropy, 22(10), 1078. https://doi.org/10.3390/e22101078
- Shutters, S. T., & Waters, K. (2020b). Industrial structure and a tradeoff between productivity and resilience. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3702545
- Waters, K., & Shutters, S. T. (2021a). Skills-approximate occupations: Using networks to guide jobs retraining. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3759962
- Waters, K., & Shutters, S. T. (2021b). Regional economic tightness from rural to populous regions [Working Paper]. https://www.statsamerica.org/research/Tightness-in-Rural-and-Populous-Regions.pdf



