Firms of a feather cluster together: The role of industry clusters on attracting additional investment
Director of Economic Analysis, Indiana Business Research Center, Indiana University Kelley School of Business
Economic Research Analyst, Indiana Business Research Center, Indiana University Kelley School of Business

There is an expression: Birds of a feather flock together. This observation and expression has something of an equivalence in economics—agglomeration of similar companies. That is, in economics, there are competitive and productivity benefits associated with the concentration and colocation of related industries—often called industry clusters. Why birds of a feather may flock and colocate together is not of our concern here, but we are interested in whether and the extent to which firms in certain industries choose to locate together.
It turns out that U.S.-based research is sparse on whether regions with specialized industry clusters—that is, industries flocking together if the reader will allow—magnetically attract investment from firms outside the region. According to theory, industry colocation creates benefits for related industries, but to what degree do these externalities attract similar or complementary firms?
To explore this question, Indiana Business Research Center (IBRC) analysts examined greenfield foreign direct investment (FDI) data at the U.S. county level (see Figure 1) and conclude that incoming firms do indeed tend to be attracted to locations that have a relatively high absolute concentration of employment in their industry cluster. In other words, firms of a feather cluster together. Second, we also found that high-tech industries have a different FDI attraction profile than non-high-tech industry clusters—an important consideration for economic development practitioners to consider as they create their development strategies. Third, several regional characteristics that are considered important by site selectors—those informing the FDI location decisions—are more salient than other regional characteristics and attributes.
Figure 1: Number of FDI projects, 2007 to 2015
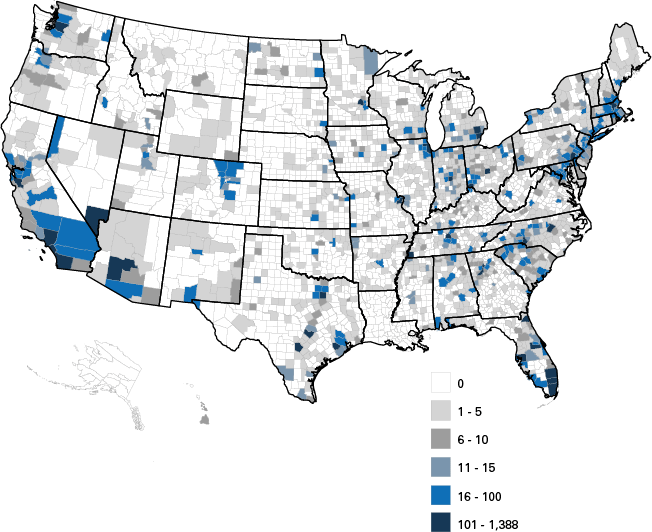
Source: Indiana Business Research Center, using fDiMarkets data
These results are largely similar and robust across several statistical methods, irrespective of whether the variable of interest (the dependent variable) is receiving FDI of any kind, the number of projects or the number of jobs associated with the FDI.
This article summarizes the main findings from this analysis. For a more complete exploration of the empirical method and regression results behind it, read the full report, “Why Invest There?,” which was funded by the Indiana University Center for International Business Education and Research (CIBER).
Background
Industry clusters—also known as business clusters or competitive clusters—are groups of similar or related firms that play an important role in the success of regional economic development. Clusters share a common market, facilitate the exchange of suppliers, and develop localized worker skills and know-how. An industry cluster represents a broadly defined industry from suppliers to end producers, which is different from the classically defined industry sectors that are organized according to production technologies.
Clusters, like cheese-making in Vermont or tech companies in California’s Silicon Valley, can strengthen competitiveness as they increase productivity, stimulate innovative new partnerships and present opportunities for entrepreneurial activity. Suppose you would like to expand your surfboard business … which is a better choice, Hawaii or Colorado? It isn’t a stretch to argue that location decisions are made due to the presence of strong industry clusters.
Industry clusters are commonly used to measure what kind of firms locate in close proximity. The empirical evidence indicates that there are competitive and productivity benefits associated with the concentration and colocation of related industries. In this article, these benefits are called colocation externalities.
It has sometimes been said that clusters form “because there is something in the air.” That something is beneficial externalities associated with similar or related firms sharing geographic proximity. Long-established firms benefit as they are effectively forced to become more productive by competitive pressures. New firms—start-ups—can also take advantage of a well-developed regional labor force and supply chain. One might say that these firms experience metabolic growth based on the resources, labor and know-how in the regions—combined with increasing demand for the cluster’s goods and services from outside the region.
On the other hand, clusters can also grow “magnetically,” that is, a region can attract firms to take advantage of that region’s competitive advantage in resources, supply networks and human talent. There might be significant benefits to close geographic proximity for young or mature firms to move into the region in order to take advantage of the colocation externalities. Greenfield FDI is an example of magnetic growth.
Either way, via metabolic growth or magnetic growth, one can understand why the concept and presence of industry clusters may attract the attention of those advocating for a region or state’s economic growth. Indeed, the importance of industry clusters to boost regional economic development has widely gained scholars’ attention, most notably, the Harvard Professor Michael Porter (1998 and 2003).
Much of the empirical work focuses on the benefits of clusters on industrial employment, innovation and productivity, but less systematic empirical attention has been paid to identifying strong regional clusters and the regional characteristics that attend cluster formation and growth. For this reason, IBRC researchers wanted to empirically confirm whether strong, established, growing clusters tended to attract incoming firms in the form of any “foreign” direct investment? (“Foreign” here is any investment from outside the region regardless of international and national.)
Industry cluster strength can be viewed as the relative concentration of an industry cluster, without regard to the balance or concentration of industries within that cluster. Economic development practitioners and policymakers often use the concept and measure of a location quotient (LQ). An LQ simply compares a proportion of industry employment in a region against some other benchmark like the national average proportion of employment in an industry. If one hears that Indiana is the most manufacturing-intensive state in the union, it isn’t because it has more workers (in absolute size) in manufacturing than, say, Texas. The claim is based on an LQ (i.e., relative size). Indiana has more workers in manufacturing as a proportion of its workforce than any other state (with Wisconsin close behind).1
While not the polar opposite of specialization, diversity is in contrast to specialization. For example, if one’s stock portfolio consists of one firm, that would be a polar opposite of diversity, but one may have a stock portfolio with all technology stocks. While specialized in technology firms, there would be some diversity of firms within that category of stocks. This latter example would be akin to a related variety of stocks. An example of unrelated variety of stocks may be one consisting of Nike, Kroger, Hilton and Sprint. Four firms in four very different markets.
In our case, a diversity of industries has both an industry cluster dimension, that is, the portfolio of industry clusters in a region, as well as the portfolio of related industries within an industry cluster. Both are akin to the diversification of stocks in a portfolio, but one is regional diversification of industry clusters, while the other is within industry cluster diversification of industries that, by classification, are aggregated into an industry cluster. In other words, cluster diversity used here is not a measure of how, and in what ways, unrelated clusters are different from each other; rather, diversity is more synonymous with industry balance within a region or within an industry cluster.
These concepts and definitions place the current investigation into context. To what degree, then, do colocation externalities motivate a firm’s decision to move into a region? Do high concentrations of related industries, or strong clusters, tend to attract additional investment inflows and thus additional employment within that cluster? In addition, we are particularly interested in whether a more diversified, or balanced, set of industries within a strong, or highly concentrated cluster tends to attract new greenfield investment or additional expansionary investment among firms already operating in the region.
One can also hypothesize about the level of the associated technological sophistication for the new employment. The investment in clusters that are not in the high-tech domain is well in evidence after the Great Recession. Initial analysis also shows that the clusters in the top 10 list in terms of the number of incoming jobs tend to be more balanced (diversified). This may signal the importance of a well-developed labor force, as well as supply chains and material linkages among colocated firms.
Finally, we also explored additional dimensions that an investor, or site selector, may consider important to a location decision: infrastructure, workforce characteristics, wages, labor market, demographics, higher education, labor regulations, taxes and incentives (International Economic Development Council, 2016). While many of these characteristics are available at the county level, the latter three items are more closely aligned with state policy and practices. If these regional or county characteristics do influence the decision to invest in one region as opposed to another, then these characteristics need to be controlled in the empirical model. Thus, to control for state policy effects, we also included state-based proxy data that investors may consider as indicators of good state governance.
Data sources and measures
Table 1 provides the list of variables used in our econometric models, which regress announced investment on plant, equipment and employment on a number of factors that characterize cluster strength.
Table 1: Source of data used in the analysis
| Data | Source | Years |
|---|---|---|
| County-level data | ||
| Employment by industry | QCEW-complete employment estimates (Indiana Business Research Center) | 2004-2015 |
| Greenfield and expansion employment | fDiMarkets | 2007-2015 |
| Number of investment projects associated with investment announcements | fDiMarkets | 2007-2015 |
| Educational attainment (percent of population with less than a high school diploma, some college, and bachelor’s degree or above) | American Community Survey (U.S. Census Bureau) |
2004-2015 |
| Percent of population in prime working ages (ages 25-44) | American Community Survey (U.S. Census Bureau) |
2004-2015 |
| Average travel time to workplace | American Community Survey (U.S. Census Bureau) |
2007-2015 |
| Number of STEM graduates | IPEDS (National Center for Education Statistics) | 2004-2015 |
| Unemployment rate | U.S. Bureau of Labor Statistics | 2004-2015 |
| Average hourly wage in manufacturing | U.S. Bureau of Labor Statistics | 2004-2015 |
| Cost of living index | Council for Community and Economic Research | 2016 |
| Transportation cost of living | Council for Community and Economic Research | 2016 |
| Interstate lane miles | U.S. Department of Transportation | 2015 |
| Cost of electricity for industrial use | U.S. Department of Energy | 2004-2015 |
| University knowledge spillovers | Indiana Business Research Center | 2010-2015 |
| State-level data | ||
| State business tax climate index | Tax Foundation | 2015 |
| State and local taxes per capita | Tax Foundation | 2012 |
| State and local tax as a percent of state income | Tax Foundation | 2012 |
| Percentage of public pension plans that are funded | Tax Foundation | 2014 |
| State credit ratings | Standard & Poors | 2004-2015 |
| Venture capital | Thompson Reuters | 2004-2015 |
Note: All the industry data are bundled into 70 “industry clusters.”
Source: Indiana Business Research Center
We used employment by industry data from QCEW-complete employment estimates, aggregating into industry clusters based upon definitions from the U.S. Cluster Mapping Project. Thus, all the industry data are bundled into “industry clusters,” of which there are 70. The proprietary data set for greenfield and expansion employment and the number of investment projects associated with investment announcements is from fDiMarkets.
There are several potential weaknesses associated with the FDI announcement data.
- The jobs realized once the plant and equipment are in operation may be different than the number of jobs reported in the press releases.
- There is no way to verify how many new, incoming magnetic jobs, were created, because of the disclosure constraints associated with record-level QCEW establishment data. In other words, one cannot link an FDI announcement record in 2012 with subsequent establishment data.
- There is no fixed time between an FDI press release and realized jobs. The latter can vary greatly depending on the industry, the scale of investment, market demand conditions for the firms, etc.
That said, firms have been known to spend several years and millions of dollars in site selection and negotiating with local and state officials before making an announcement; thus, we consider the FDI announcements as an appropriate signal for a region’s relative attractiveness in terms of agglomeration externalities.
The unit of analysis is industry clusters at the U.S. county level. Some FDI projects could be considered “local”—for example, real estate development or consumer banking branches—in contrast to “traded” industries, for which the market generally extends beyond the region. The vast majority of FDI announcements are for traded industries, and we consider only traded industry clusters in this analysis. We collected nine years of FDI data (2007 to 2015), grouping them into three three-year time periods since FDI data by county tends to be sparse. Of the 30,774 FDI announced events in the U.S. over this time period, 20,632 were in the relevant traded industries.
There are 243,698 county-by-industry-cluster observations for the 2007 to 2015 time period, implying that the average county has about 27 traded industry clusters, based on the QCEW-complete data. Around 40 percent of those county-industry clusters are sufficiently concentrated in the “cluster development strategy” sense. About 14 percent of these are high-tech industries.
County-by-industry-clusters can have multiple projects or FDI attraction events over the time period. As a result, the number of county-by-industry-clusters that recorded FDI employment announcements is whittled down to 8,194. The average number of jobs per FDI announcement is 190, but each FDI project or event can range from one new job to over 8,000. For an example of the latter, the IT sector in Travis County, Texas, (i.e., Austin) attracted 8,000 new workers based on an FDI announcement.
While the main data source for the explanatory variables is QCEW data by industry, how these data are operationalized to provide measures of regional agglomeration and industry structure warrants discussion.
There is a wide variation in terms for cluster concentration/specialization. For example, farming regions and regions endowed with natural resources tend to have very high employment concentrations in specialized sectors. On the other hand, high-tech clusters, especially the ones associated with FDI—for example, Travis County, Texas—tend to have a more diversified economy and industrial profile.
We use a common entropy measure—the Shannon Evenness Index—to assess the degree to which a region’s industry clusters are even/balanced or uneven. An index value of zero (perfect unevenness) occurs if there is only one industry in the region, whereas 1 denotes a perfect balance among industry clusters.
We used two variables for industry cluster strength, or specialization: the value of the location quotient (calculated as the proportion of an industry's employment relative to the national average proportion of employment in the industry) and a binary threshold to indicate high strength (i.e., whether the location quotient exceeds 1.2).
The three measures discussed above are related to how even/balanced industry clusters are among themselves. These are measures “outside” a particular industry cluster. The next two measures (an industrial Shannon index and industrial imbalance score) address the balance, evenness or industry specialization within a cluster, providing a glimpse into how the industry concentrations deviate from the national averages. As discussed earlier, the concern is the degree to which an industry cluster in a particular region has the same relative concentration of industries as the nation. Does an industry cluster that is dominated by one particular industry in that cluster yield the same magnetic attraction as an industry cluster that is more balanced? Does a wider complement of industries influence investment decisions?
Finally, in order to provide the reader a sense of the impact of FDI events across the county, Figure 2 presents reported FDI employment growth, while Figure 3 shows planned FDI investment in dollars. Both FDI employment and dollar investment show higher concentrations along the coasts, as well as in the Great Lakes and South regions. The FDI also tends to go to more populated areas, such as Phoenix in Arizona and Dallas and the Austin–San Antonio–Houston triangle in Texas.
Figure 2: Anticipated FDI employment gains, 2007 to 2015
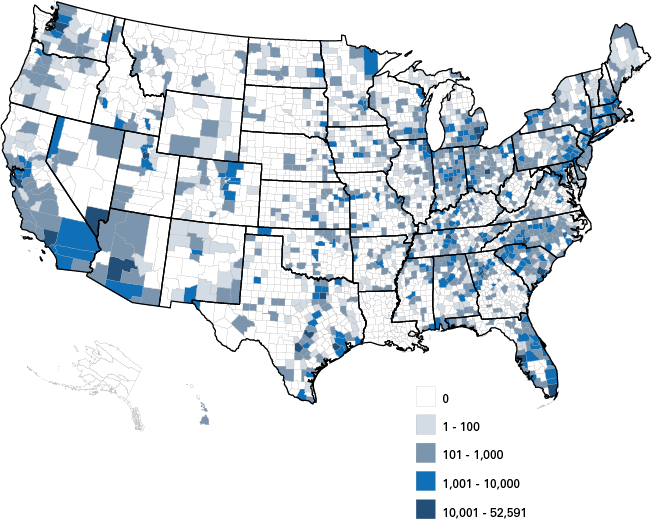
Source: Indiana Business Research Center, using fDiMarkets data
Figure 3: Planned FDI investments (in millions of dollars), 2007 to 2015
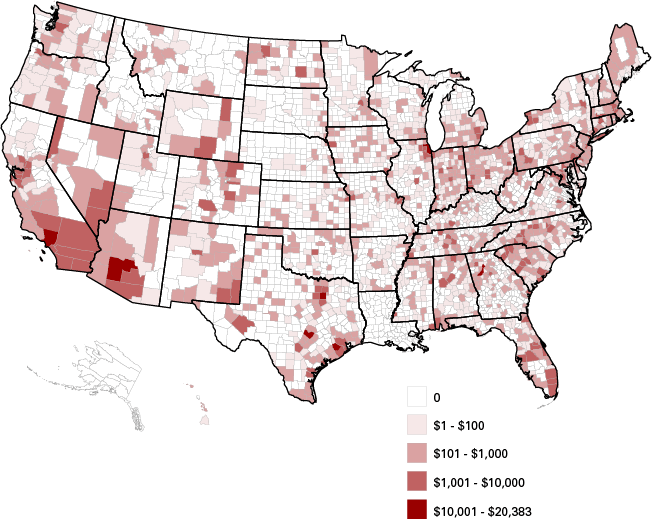
Source: Indiana Business Research Center, using fDiMarkets data
Analysis and results
We explored empirically the “magnetic” growth of county-clusters via three venues: whether it happens (delineated as the odds that a county has received FDI investment), and if so, how often it happens (delineated as the number of projects invested), and how large is the investment (delineated as the employment growth made by such investments). These three analytical approaches are closely related, but each sheds its own insight. We estimated the FDI employment growth by the method of ordinary least squares (OLS) in Model 1, the odds of receiving FDI investment by the logit model in Model 2 and project investment by the negative binomial model in Model 3.
Model 1
Our hypotheses were confirmed. Investment in a county as measured by employment growth attributed to greenfield FDI is strongly positively associated with the absolute size of clusters—i.e., the bigger a cluster, the greater the magnetic attraction of FDI-related employment. The model estimated that a 1 percent increase in industrial cluster employment is associated with a nearly 30 percent increase in FDI employment. That said, the marginal effect is higher for non-high-tech clusters relative to high-tech clusters.
Cluster strength is also positively associated with the growth of FDI employment, and this is largely driven by high-concentration clusters (those with LQ > 1.2). The evidence suggests that specialization in an industry cluster serves as a magnet for FDI-related employment. Low-concentration industry clusters, that is, those with a relatively weak presence of cluster aggregate employment in a region, can have a negative effect on attracting FDI employment. Considering that a vast majority of counties have an LQ below 1 for most of a county’s industry clusters, this result is not surprising.
Industry cluster diversity, or evenness across clusters, in a county is negatively associated with FDI-related employment. That is, those regions that specialize in one or two industry clusters (i.e., less diversified/balanced) tend to receive more FDI-related employment. This effect, however, is mainly driven by high-tech clusters. In general, high-tech industry clusters tend to gain more FDI-related employment than non-high-tech clusters.
The measure of balance for the industries that make up an industry cluster, is negatively associated with FDI. Put another way, specialization within a cluster is positive and statistically significant. However, this effect is offset by the negative effect from the interaction term for high-tech, suggesting that industries in high-tech industry clusters appear to benefit from a more balanced industrial profile for attracting FDI employment. Conversely, industry clusters that are not high-tech would not be penalized for the lack of within-cluster diversity or evenness.
Leaving the magnetic benefits of agglomeration aside for a moment, several regional characteristics may also influence attracting FDI employment. The cost of living in a region does not seem to matter much in relation to the employment flow from FDI once the state-level characteristics are considered. How educational attainment affects FDI is ambiguous. However, the presence of a robust educational system, measured by the share of STEM graduates in the population, may positively influence FDI deicsions. High shares of prime-working-age population and high unemployment rates also seem to attract more FDI, indicating that FDI decision makers are interested in locations with abundant labor. Venture capital and FDI inflows tend to move together.
Interpreting the worker commute time (i.e., mean travel time to work) is difficult. Increases in mean travel time may indicate congestion in cities—a negative. On the other hand, long commutes from one rural county to another or from one exurb to another may indicate a degree of labor flexibility and a larger labor shed from which to draw talent.
State-level characteristics that may be relevant to location decisions, such as electricity cost and tax burden measures, were incorporated into the models. It appears that only electricity cost has a strong association with FDI employment—a 1 percent increase in electricity cost is associated with a 26 percent decrease in FDI employment. Of the several measures for good state governance, business conditions and taxes, only state and local taxes appear to have an influence.
Model 2
The logit model estimated the odds of attracting FDI projects—all projects, whether large or small are counted the same—based on the same variables in Model 1. The effects of the absolute size of cluster employment, within-cluster specialization and high-tech are similar to that of the first model. Where the results diverge are the relative measures of cluster strength, or specialization. Neither the variable indicating the presence of a highly concentrated cluster (with LQ > 1.2) nor the relative concentration of a cluster has much to do with site selection. The odds of attracting FDI projects also do not seem to depend on the interplay between the size of the industry cluster and whether the cluster in the region is high-tech or not. For Model 2, educational attainment emerges as a factor in increasing the chances of attracting FDI projects. A higher proportion of the population without a high school degree reduces the chances, while having a greater proportion of a region’s population with a bachelor’s degree or higher increases the odds of attracting FDI projects.
The size of a county as measured by total county employment emerges as increasing the odds of attracting FDI projects, as does relative proximity to universities engaged in STEM-related research and development, as measured by university knowledge spillovers within 50 miles of universities (Zheng and Slaper, 2017). Mean travel time reduces a region’s chances, while one measure for infrastructure availability, interstate lane miles per capita, increases a region’s attractiveness. Finally, in terms of good governance measures, a state’s credit rating positively influences a region’s chances for attracting FDI projects.
Model 3
The negative binomial model2 estimated the number of FDI projects a county-cluster received. Overall, the results were similar to the case of FDI-related employment, such as cluster employment and cluster balance. Unlike the previous case, we found high-tech industries do not necessarily receive more investment projects than non-high-tech ones. That said, the number of projects and the number of new workers associated with those projects can deviate considerably. The cost of living is positively related to the number of projects, contrary to expectations.
The only educational attainment measure with statistical significance is for some college, and then it has a negative sign, contrary to expectations. Then again, if a majority of projects are for manufacturing plants that do not require a highly educated workforce, the negative relationship between university education and project counts may not be counterintuitive. The sign for the proximity to university R&D is also contrary to expectations, but may be explained in the same way as education. However, it is difficult to make the latter two results square with the number of STEM-degree graduates from institutions in the region as positively related to the number of projects a region attracted.
The relationship with interstate lane miles per capita is negative, but this may be indicative of many projects sited in rural counties, far removed from dense development. Rural locations of projects may also help to explain why mean travel time is positively related to the number of FDI projects attracted. As for state characteristics, higher electricity costs are associated with fewer FDI projects, but, contrary to expectations, both state and local taxes per capita and the ratio of state pension plans that are funded are marginally negative (and significant). That said, a good business climate is positively associated with attracting FDI projects.
Additional models
We also attempted to identify the source of variation that contributes to differences in FDI. For those who are interested in statistics and econometrics, the approach is called a pseudo-panel model. Without getting too fancy with the explanation, we compare clusters across two dimensions—time and space (or county). The goal of the analysis is to see if the source of FDI variation is the (possible) change of cluster characteristics over time or if the variation is a result in the differences among regions.
This model shows that the across-time variation of most of the explanatory variables are not significantly associated with FDI employment, with a few exceptions. The sectors that have higher rates of unemployment would attract more FDI employment and so would regions that have more highly educated workers. On the other hand, large high-tech clusters and regions with more prime-working-age populations may reduce the inflow of FDI employment over time. Overall, the assessment of model fit suggests that time variation is not a significant source in explaining FDI employment attraction. This leads to the conclusion that the explanatory power of the characteristics associated with attracting FDI employment is better explained by the cross-sectional variation across the industry cluster space.
Indeed, results from the cross-sectional examination of FDI-related employment variation, removing the time-varying component, are very similar to that of the OLS model.
In the second panel setup, we eliminated the time dimension and focused on the differences in region (county) and clusters. The marginal effects from industry cluster-specific characteristics (i.e., within-cluster variations) have become much stronger (highly significant and larger). This leads to the conclusion that industry cluster effects are more dominant than regional characteristics for FDI location decisions.
Discussion and conclusion
Whether site selectors or corporate decision makers are aware of it or not, the location of FDI projects is not greatly decided by industry cluster specialization, but align with the benefits of highly concentrated clusters, which magnetically attract incoming investment into counties. And whether the industry cluster is high-tech or not may dictate if a region needs to have a balanced, diversified cluster or if specialization in one particular industry within a cluster can be sufficient to attract FDI employment.
Also, certain regional or state characteristics may be important in attracting FDI according to our findings. FDI decisions in educational attainment may relate to the scale and nature of the activity—a small high-tech firm may not consider this an important consideration, but for a 2,000-person manufacturing plant, it is critical. A “flexible” labor market may be an important consideration when considering the scale of a facility: higher unemployment, a large share of prime-working-age population and longer travel time to work may indicate sufficient slack in the labor shed to induce larger facilities to locate in a region. A state’s higher credit score may indicate the ability of a state government to negotiate favorable terms with the firm on tax breaks or worker training and retention incentives. Without more granular, case-specific information, these statements are nothing more than hypotheses, but based on our findings, these are credible research paths to explore.
Absent consistent data for site availability or deal-specific details on the incentives—tax reduction benefits or worker hiring and training inducements—to locate in a particular region, the data on FDI location decisions would indicate that colocation economies, lower electricity costs and good state governance conditions drive where greenfield investment and expansions occur.
In summary, we have tested and found valid the claims that the economies of colocation serve as one inducement, among several considerations, for firms to locate in one region as opposed to another. Moreover, these economies of colocation are associated with the absolute scale of the firms in geographic proximity, rather than the relative concentration of those firms within a region.
We have also found that a firm within a specifically defined industrial category may be attracted to regions with other firms in close proximity within the same, specific, industrial category. But this depends on the type of industry. For example, high-tech firms appear to seek the presence of a cluster that is internally well-balanced. In contrast, internal cluster balance does not appear to be a concern for non-high-tech firms.
Finally, we have found several important regional and state characteristics that appear to have motivated FDI decisions. Electricity costs have a strong association with FDI employment and state and local taxes also appear to have an influence on site location decisions.
For complete details on this analysis and the regression results, read the full report, “Why Invest There?,” at www.ibrc.indiana.edu/studies/why-invest-there-2018.pdf.
References
- Ellison, G., & Glaeser, E. L. (1997). Geographic concentration in U.S. manufacturing industries: A dartboard approach. Journal of Political Economy, 105(5), 889-927.
- International Economic Development Council. (2016). A new standard: Achieving data excellence in economic development. Washington, DC: Author.
- Marshall, A. (1966). Principles of economics (8th ed.). London: Macmillan.
- Porter, M. E. (1998). Clusters and competition: New agendas for companies, governments, and institutions. In M. E. Porter (Ed.), On competition (pp. 197–299). Boston, MA: Harvard Business School Press.
- Porter, M. E. (2003). The economic performance of regions. Regional Studies 37, 549–578.
- Zheng, P., & Slaper, T. F. (2016). University knowledge spillovers, geographic proximity and innovation: An analysis of patent filings across U.S. counties. [Presentation]. Paper presented at the 63th Annual North American Meetings of the Regional Science Association International. Minneapolis, MN. Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2857130
Notes
- The LQ isn’t the last word, or metric, in terms of specialization. Many researchers make the case that specialization (or concentration) is better measured based on absolute size rather than location quotient because, depending on the industry, a region needs a critical mass of employment to be considered specialized in an industry.
- Negative binomial regression is similar to regular multiple regression except that the dependent (Y) variable is an observed count that follows the negative binomial distribution. Thus, the possible values of Y are the nonnegative integers: 0, 1, 2, 3, and so on. Negative binomial regression is often used for over-dispersed count data. That is, if the counts are highly uneven across observations/counties and there are many zero counts, as is the case with 3,110 counties in the U.S., negative binomial regression is often the preferred statistical method.



